Mersenne prime
| Named after | Marin Mersenne |
|---|---|
| Publication year | 1536[1] |
| Author of publication | Regius, H. |
| Number of known terms | 47 |
| Conjectured number of terms | Infinite |
| Subsequence of | Mersenne numbers |
| First terms | 3, 7, 31, 127 |
| Largest known term | 243112609 − 1 |
| OEIS index | A000668 |
In mathematics, a Mersenne number, named after Marin Mersenne (a French monk who began the study of these numbers in the early 17th century), is a positive integer that is one less than a power of two:
Some definitions of Mersenne numbers require that the exponent p be prime, since the associated number must be composite if p is composite.
A Mersenne prime is a Mersenne number that is prime. It is known[2] that if 2p − 1 is prime then p is prime, so it makes no difference which Mersenne number definition is used. As of October 2009[ref], 47 Mersenne primes are known. The largest known prime number (243,112,609 – 1) is a Mersenne prime.[3] Since 1997, all newly-found Mersenne primes have been discovered by the "Great Internet Mersenne Prime Search" (GIMPS), a distributed computing project on the Internet.
Contents |
About Mersenne primes
| Are there infinitely many Mersenne primes? |
Many fundamental questions about Mersenne primes remain unresolved. It is not even known whether the set of Mersenne primes is finite. The Lenstra–Pomerance–Wagstaff conjecture asserts that, on the contrary, there are infinitely many Mersenne primes and predicts their order of growth. It is also not known whether infinitely many Mersenne numbers with prime exponents are composite, although this would follow from widely believed conjectures about prime numbers, for example, the infinitude of Sophie Germain primes congruent to 3 (mod 4).
A basic theorem about Mersenne numbers states that in order for Mp to be a Mersenne prime, the exponent p itself must be a prime number. This rules out primality for numbers such as M4 = 24 − 1 = 15: since the exponent 4 = 2×2 is composite, the theorem predicts that 15 is also composite; indeed, 15 = 3×5. The three smallest Mersenne primes are
- M2 = 3, M3 = 7, M5 = 31.
While it is true that only Mersenne numbers Mp, where p = 2, 3, 5, … could be prime, Mp is very rarely prime even for a prime exponent p. The smallest counterexample is the Mersenne number
- M11 = 211 − 1 = 2047 = 23 × 89,
which is not prime, even though 11 is a prime number. The lack of an obvious rule to determine whether a given Mersenne number is prime makes the search for Mersenne primes an interesting task, which becomes difficult very quickly, since Mersenne numbers grow very rapidly. The Lucas–Lehmer primality test (LLT) is an efficient primality test that greatly aids this task. The search for the largest known prime has somewhat of a cult following. Consequently, a lot of computer power has been expended searching for new Mersenne primes, much of which is now done using distributed computing.
Mersenne primes are used in pseudorandom number generators such as the Mersenne twister, Park–Miller random number generator, Generalized Shift Register and Fibonacci RNG.
Searching for Mersenne primes
The identity
shows that Mp can be prime only if p itself is prime, which simplifies the search for Mersenne primes considerably. The converse statement, namely that Mp is necessarily prime if p is prime, is false. The smallest counterexample is 211 − 1 = 2,047 = 23 × 89, a composite number.
Fast algorithms for finding Mersenne primes are available, and the largest known prime numbers as of 2009 are Mersenne primes.
The first four Mersenne primes M2 = 3, M3 = 7, M5 = 31 and M7 = 127 were known in antiquity. The fifth, M13 = 8191, was discovered anonymously before 1461; the next two (M17 and M19) were found by Cataldi in 1588. After nearly two centuries, M31 was verified to be prime by Euler in 1772. The next (in historical, not numerical order) was M127, found by Lucas in 1876, then M61 by Pervushin in 1883. Two more (M89 and M107) were found early in the 20th century, by Powers in 1911 and 1914, respectively.
The best method presently known for testing the primality of Mersenne numbers is the Lucas–Lehmer primality test. Specifically, it can be shown that for prime p > 2, Mp = 2p − 1 is prime if and only if Mp divides Sp−2, where S0 = 4 and, for k > 0,
The search for Mersenne primes was revolutionized by the introduction of the electronic digital computer. Alan Turing searched for them on the Manchester Mark 1 in 1949.[4] But the first successful identification of a Mersenne prime, M521, by this means was achieved at 10:00 P.M. on January 30, 1952 using the U.S. National Bureau of Standards Western Automatic Computer (SWAC) at the Institute for Numerical Analysis at the University of California, Los Angeles, under the direction of Lehmer, with a computer search program written and run by Prof. R.M. Robinson. It was the first Mersenne prime to be identified in thirty-eight years; the next one, M607, was found by the computer a little less than two hours later. Three more — M1279, M2203, M2281 — were found by the same program in the next several months. M4253 is the first Mersenne prime that is titanic, M44497 is the first gigantic, and M6,972,593 was the first megaprime to be discovered, being a prime with at least 1,000,000 digits.[5] All three were the first known prime of any kind of that size.
In September 2008, mathematicians at UCLA participating in GIMPS won part of a $100,000 prize from the Electronic Frontier Foundation for their discovery of a very nearly 13-million-digit Mersenne prime. The prize, finally confirmed in October 2009, is for the first known prime with at least 10 million digits. The prime was found on a Dell OptiPlex 745 on August 23, 2008. This is the eighth Mersenne prime discovered at UCLA.[6]
On April 12, 2009, a GIMPS server log reported that a 47th Mersenne prime had possibly been found. This report was apparently overlooked until June 4, 2009. The find was verified on June 12, 2009. The prime is 242,643,801 − 1. Although it is chronologically the 47th Mersenne prime to be discovered, it is less than the largest known which was the 45th to be discovered.
Theorems about Mersenne numbers
- If a and p are natural numbers such that ap − 1 is prime, then a = 2 or p = 1.
- Proof: a ≡ 1 (mod a − 1). Then ap ≡ 1 (mod a − 1), so ap − 1 ≡ 0 (mod a − 1). Thus a − 1 | ap − 1. However, ap − 1 is prime, so a − 1 = ap − 1 or a − 1 = ±1. In the former case, a = ap, hence a = 0,1 (which is a contradiction, as neither 1 nor 0 is prime) or p = 1. In the latter case, a = 2 or a = 0. If a = 0, however, 0p − 1 = 0 − 1 = −1 which is not prime. Therefore, a = 2.
- If 2p − 1 is prime, then p is prime.
- Proof: suppose that p is composite, hence can be written p = a⋅b with a and b > 1. Then (2a)b − 1 is prime, but b > 1 and 2a > 2, contradicting statement 1.
- If p is an odd prime, then any prime q that divides 2p − 1 must be 1 plus a multiple of 2p. This holds even when 2p − 1 is prime.
- Examples: Example I: 25 − 1 = 31 is prime, and 31 = 1 + 3×2×5. Example II: 211 − 1 = 23×89, where 23 = 1 + 2×11, and 89 = 1 + 4×2×11.
- Proof: If q divides 2p − 1 then 2p ≡ 1 (mod q). By Fermat's Little Theorem, 2(q − 1) ≡ 1 (mod q). Assume p and q − 1 are relatively prime, a similar application of Fermat's Little Theorem says that (q − 1)(p − 1) ≡ 1 (mod p). Thus there is a number x ≡ (q − 1)(p − 2) for which (q − 1)·x ≡ 1 (mod p), and therefore a number k for which (q − 1)·x − 1 = kp. Since 2(q − 1) ≡ 1 (mod q), raising both sides of the congruence to the power x gives 2(q − 1)x ≡ 1, and since 2p ≡ 1 (mod q), raising both sides of the congruence to the power k gives 2kp ≡ 1. Thus 2(q − 1)x/2kp = 2(q − 1)x − kp ≡ 1 (mod q). But by definition, (q − 1)x − kp = 1, implying that 21 ≡ 1 (mod q); in other words, that q divides 1. Thus the initial assumption that p and q − 1 are relatively prime is untenable. Since p is prime q − 1 must be a multiple of p. Of course, if the number m = (q − 1)⁄p is odd, then q will be even, since it is equal to mp + 1. But q is prime and cannot be equal to 2; therefore, m is even.
- Note: This fact provides a proof of the infinitude of primes distinct from Euclid's Theorem: if there were finitely many primes, with p being the largest, we reach an immediate contradiction since all primes dividing 2p − 1 must be larger than p.
- If p is an odd prime, then any prime q that divides
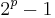 must be congruent to
must be congruent to 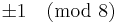 .
.
- Proof:
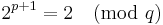 , so
, so 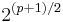 is a square root of 2 modulo
is a square root of 2 modulo  . By quadratic reciprocity, any prime modulo which 2 has a square root is congruent to
. By quadratic reciprocity, any prime modulo which 2 has a square root is congruent to 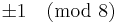 .
.
- Proof:
- A Mersenne prime cannot be a Wieferich prime.
- Proof: We show if
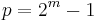 is a Mersenne prime, then the congruence
is a Mersenne prime, then the congruence 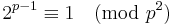 does not satisfy. By Fermat's Little theorem,
does not satisfy. By Fermat's Little theorem, 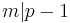 . Now write,
. Now write, 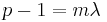 . If the given congruence satisfies, then
. If the given congruence satisfies, then 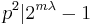 ,therefore
,therefore 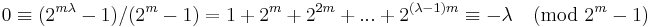 . Hence
. Hence 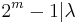 ,and therefore λ ≥ 2m − 1. This leads to p − 1 ≥ m(2m − 1), which is impossible since m ≥ 2.
,and therefore λ ≥ 2m − 1. This leads to p − 1 ≥ m(2m − 1), which is impossible since m ≥ 2.
- Proof: We show if
- A prime number divides at most one prime-exponent Mersenne number[7]
History
Mersenne primes were considered already by Euclid, who found a connection with the perfect numbers. They are named after 17th-century French scholar Marin Mersenne, who compiled what was supposed to be a list of Mersenne primes with exponents up to 257. His list was largely incorrect, as Mersenne mistakenly included M67 and M257 (which are composite), and omitted M61, M89, and M107 (which are prime). Mersenne gave little indication how he came up with his list.[8] A correct list of all Mersenne primes in this number range was completed and rigorously verified only about three centuries later. M61 was determined to be prime in 1883 by Ivan Mikheevich Pervushin and for this reason it is sometimes called Pervushin's number. At the time of Pervushin's proof it was the second-largest known prime number, (Édouard Lucas having shown earlier that M127 is also prime), and it remained so until 1911.
List of known Mersenne primes
The table below lists all known Mersenne primes (sequence A000668 in OEIS):
| # | p | Mp | Mp digits | Date of discovery | Discoverer | Method used |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | c. 500 BCE[9] | Ancient Greek mathematicians | |
| 2 | 3 | 7 | 1 | c. 500 BCE[9] | Ancient Greek mathematicians | |
| 3 | 5 | 31 | 2 | c. 275 BCE[9] | Ancient Greek mathematicians | |
| 4 | 7 | 127 | 3 | c. 275 BCE[9] | Ancient Greek mathematicians | |
| 5 | 13 | 8191 | 4 | 1456 | Anonymous[2] | Trial division |
| 6 | 17 | 131071 | 6 | 1588 | Pietro Cataldi | Trial division |
| 7 | 19 | 524287 | 6 | 1588 | Pietro Cataldi | Trial division |
| 8 | 31 | 2147483647 | 10 | 1772 | Leonhard Euler[10] [11] | Enhanced trial division[12] |
| 9 | 61 | 2305843009213693951 | 19 | 1883 | I. M. Pervushin | Lucas sequences |
| 10 | 89 | 618970019…449562111 | 27 | 1911 June[13] | R. E. Powers | Lucas sequences |
| 11 | 107 | 162259276…010288127 | 33 | 1914 June 11[14] | R. E. Powers[15] | Lucas sequences |
| 12 | 127 | 170141183…884105727 | 39 | 1876 January 10[16] | Édouard Lucas | Lucas sequences |
| 13 | 521 | 686479766…115057151 | 157 | 1952 January 30 | Raphael M. Robinson | LLT / SWAC |
| 14 | 607 | 531137992…031728127 | 183 | 1952 January 30 | Raphael M. Robinson | LLT / SWAC |
| 15 | 1,279 | 104079321…168729087 | 386 | 1952 June 25 | Raphael M. Robinson | LLT / SWAC |
| 16 | 2,203 | 147597991…697771007 | 664 | 1952 October 7 | Raphael M. Robinson | LLT / SWAC |
| 17 | 2,281 | 446087557…132836351 | 687 | 1952 October 9 | Raphael M. Robinson | LLT / SWAC |
| 18 | 3,217 | 259117086…909315071 | 969 | 1957 September 8 | Hans Riesel | LLT / BESK |
| 19 | 4,253 | 190797007…350484991 | 1,281 | 1961 November 3 | Alexander Hurwitz | LLT / IBM 7090 |
| 20 | 4,423 | 285542542…608580607 | 1,332 | 1961 November 3 | Alexander Hurwitz | LLT / IBM 7090 |
| 21 | 9,689 | 478220278…225754111 | 2,917 | 1963 May 11 | Donald B. Gillies | LLT / ILLIAC II |
| 22 | 9,941 | 346088282…789463551 | 2,993 | 1963 May 16 | Donald B. Gillies | LLT / ILLIAC II |
| 23 | 11,213 | 281411201…696392191 | 3,376 | 1963 June 2 | Donald B. Gillies | LLT / ILLIAC II |
| 24 | 19,937 | 431542479…968041471 | 6,002 | 1971 March 4 | Bryant Tuckerman | LLT / IBM 360/91 |
| 25 | 21,701 | 448679166…511882751 | 6,533 | 1978 October 30 | Landon Curt Noll & Laura Nickel | LLT / CDC Cyber 174 |
| 26 | 23,209 | 402874115…779264511 | 6,987 | 1979 February 9 | Landon Curt Noll | LLT / CDC Cyber 174 |
| 27 | 44,497 | 854509824…011228671 | 13,395 | 1979 April 8 | Harry Lewis Nelson & David Slowinski | LLT / Cray 1 |
| 28 | 86,243 | 536927995…433438207 | 25,962 | 1982 September 25 | David Slowinski | LLT / Cray 1 |
| 29 | 110,503 | 521928313…465515007 | 33,265 | 1988 January 28 | Walter Colquitt & Luke Welsh | LLT / NEC SX-2[17] |
| 30 | 132,049 | 512740276…730061311 | 39,751 | 1983 September 19[9] | David Slowinski | LLT / Cray X-MP |
| 31 | 216,091 | 746093103…815528447 | 65,050 | 1985 September 1[9] | David Slowinski | LLT / Cray X-MP/24 |
| 32 | 756,839 | 174135906…544677887 | 227,832 | 1992 February 19 | David Slowinski & Paul Gage | LLT / Maple on Harwell Lab Cray-2[18] |
| 33 | 859,433 | 129498125…500142591 | 258,716 | 1994 January 4[19] | David Slowinski & Paul Gage | LLT / Cray C90 |
| 34 | 1,257,787 | 412245773…089366527 | 378,632 | 1996 September 3 | David Slowinski & Paul Gage[20] | LLT / Cray T94 |
| 35 | 1,398,269 | 814717564…451315711 | 420,921 | 1996 November 13 | GIMPS / Joel Armengaud[21] | LLT / Prime95 on 90 MHz Pentium PC |
| 36 | 2,976,221 | 623340076…729201151 | 895,932 | 1997 August 24 | GIMPS / Gordon Spence[22] | LLT / Prime95 on 100 MHz Pentium PC |
| 37 | 3,021,377 | 127411683…024694271 | 909,526 | 1998 January 27 | GIMPS / Roland Clarkson[23] | LLT / Prime95 on 200 MHz Pentium PC |
| 38 | 6,972,593 | 437075744…924193791 | 2,098,960 | 1999 June 1 | GIMPS / Nayan Hajratwala[24] | LLT / Prime95 on 350 MHz IBM Aptiva |
| 39 | 13,466,917 | 924947738…256259071 | 4,053,946 | 2001 November 14 | GIMPS / Michael Cameron[25] | LLT / Prime95 on 800 MHz Athlon T-Bird |
| 40 | 20,996,011 | 125976895…855682047 | 6,320,430 | 2003 November 17 | GIMPS / Michael Shafer[26] | LLT / Prime95 on 2 GHz Dell Dimension |
| 41 | 24,036,583 | 299410429…733969407 | 7,235,733 | 2004 May 15 | GIMPS / Josh Findley[27] | LLT / Prime95 on 2.4 GHz Pentium 4 PC |
| 42[*] | 25,964,951 | 122164630…577077247 | 7,816,230 | 2005 February 18 | GIMPS / Martin Nowak[28] | LLT / Prime95 on 2.4 GHz Pentium 4 PC |
| 43[*] | 30,402,457 | 315416475…652943871 | 9,152,052 | 2005 December 15 | GIMPS / Curtis Cooper & Steven Boone[29] | LLT / Prime95 on 2 GHz Pentium 4 PC |
| 44[*] | 32,582,657 | 124575026…053967871 | 9,808,358 | 2006 September 4 | GIMPS / Curtis Cooper & Steven Boone[30] | LLT / Prime95 on 3 GHz Pentium 4 PC |
| 45[*] | 37,156,667 | 202254406…308220927 | 11,185,272 | 2008 September 6 | GIMPS / Hans-Michael Elvenich[31] | LLT / Prime95 on 2.83 GHz Core 2 Duo PC |
| 46[*] | 42,643,801 | 169873516…562314751 | 12,837,064 | 2009 April 12[**] | GIMPS / Odd M. Strindmo | LLT / Prime95 on 3 GHz Core 2 PC |
| 47[*] | 43,112,609 | 316470269…697152511 | 12,978,189 | 2008 August 23 | GIMPS / Edson Smith[31] | LLT / Prime95 on Dell Optiplex 745 |
* It is not known whether any undiscovered Mersenne primes exist between the 41st (M24,036,583) and the 47th (M43,112,609) on this chart; the ranking is therefore provisional. Primes are not always discovered in increasing order. For example, the 29th Mersenne prime was discovered after the 30th and the 31st. Similarly, the current record holder was followed by two smaller Mersenne primes, first 2 weeks later and then 8 months later.
** M42,643,801 was first found by a machine on April 12, 2009; however, no human took notice of this fact until June 4. Thus, either April 12 or June 4 may be considered the 'discovery' date. The discoverer, Strindmo, apparently used the alias Stig M. Valstad.
To help visualize the size of the 47th known Mersenne prime, it would require 3,461 pages to display the number in base 10 with 75 digits per line and 50 lines per page.[9]
The largest known Mersenne prime (243,112,609 − 1) is also the largest known prime number,[3] and was the first discovered prime number with more than 10 million base-10 digits.
In modern times, the largest known prime has almost always been a Mersenne prime.[32]
Factorization of Mersenne numbers
The factorization of a prime number is by definition the number itself. This section is about composite numbers. Mersenne numbers are very good test cases for the special number field sieve algorithm, so often the largest number factorized with this algorithm has been a Mersenne number. As of March 2007[update], 21039 − 1 is the record-holder,[33] after a calculation taking about a year on a couple of hundred computers, mostly at NTT in Japan and at EPFL in Switzerland. See integer factorization records for links to more information. The special number field sieve can factorize numbers with more than one large factor. If a number has only one very large factor then other algorithms can factorize larger numbers by first finding small factors and then making a primality test on the cofactor. As of December 2011[update], the composite Mersenne number with largest proven prime factors is 226903 − 1 = 1113285395642134415541632833178044793 × p, where p has 8063 digits and was proven prime with ECPP.[34] The largest factorization with probable prime factors allowed is 21168183 − 1 = 54763676838381762583 × q, where q is a 351639-digit probable prime.[35]
Perfect numbers
Mersenne primes are interesting to many for their connection to perfect numbers. In the 4th century BCE, Euclid demonstrated that if Mp is a Mersenne prime then
is an even perfect number (Elements ix.36)—which is also the Mpth triangular number and the 2p−1th hexagonal number. In the 18th century, Leonhard Euler proved that, conversely, all even perfect numbers have this form. It is unknown whether there are any odd perfect numbers, but it appears unlikely.
Generalization
The binary representation of 2p − 1 is the digit 1 repeated p times, for example, 25 − 1 = 111112 in the binary notation. A Mersenne number is therefore a repunit in base 2, and Mersenne primes are the base 2 repunit primes.
The base 2 representation of a Mersenne number shows the factorization pattern for composite exponent. For example:
Mersenne numbers in nature and elsewhere
In computer science, unsigned p-bit (or signed p+1-bit) integers can be used to express numbers up to Mp.
In the mathematical problem Tower of Hanoi, solving a puzzle with a p-disc tower requires at least Mp steps.
The asteroid with minor planet number 8191 is named 8191 Mersenne after Marin Mersenne, because 8191 is a Mersenne prime (3 Juno, 7 Iris, 31 Euphrosyne and 127 Johanna having been discovered and named during the nineteenth century).[36]
See also
References
- ^ Regius, Hudalricus. Utrisque Arithmetices Epitome. http://books.google.de/books?id=hs85AAAAcAAJ&printsec=frontcover&dq=Utriusque+Arithmetices+epitome&hl=de&ei=o4cDTb10y_WyBur_8PkJ&sa=X&oi=book_result&ct=result&resnum=1&ved=0CCoQ6AEwAA#v=onepage&q=2047&f=false.
- ^ a b The Prime Pages, Mersenne Primes: History, Theorems and Lists.
- ^ a b "12-million-digit prime number sets record, nets $100,000 prize". Networkworld.com. http://www.networkworld.com/community/node/46184. Retrieved 2011-05-21.
- ^ Brian Napper, The Mathematics Department and the Mark 1.
- ^ The Prime Pages, The Prime Glossary: megaprime.
- ^ "UCLA mathematicians discover a 13-million-digit prime number". Los Angeles Times. 2008-09-27. http://www.latimes.com/news/science/la-sci-prime27-2008sep27,0,2746766.story. Retrieved 2011-05-21.
- ^ Will Edgington's Mersenne Page
- ^ The Prime Pages, Mersenne's conjecture.
- ^ a b c d e f g Landon Curt Noll, Mersenne Prime Digits and Names.
- ^ http://bibliothek.bbaw.de/bbaw/bibliothek-digital/digitalequellen/schriften/anzeige/index_html?band=03-nouv/1772&seite:int=36 Nouveaux Mémoires de l'Académie Royale des Sciences et Belles-Lettres 1772, pp. 35-36 EULER, Leonhard: Extrait d'une lettre à M. Bernoulli, concernant le Mémoire imprimé parmi ceux de 1771. p. 318 [intitulé: Recherches sur les diviseurs de quelques nombres très grands compris dans la somme de la progression géométrique 1+101+102+103+...10T=S]. Retrieved 2011-10-02.
- ^ http://primes.utm.edu/notes/by_year.html#31 The date and year of discovery is unsure. Dates between 1752 and 1772 are possible.
- ^ Chris K. Caldwell. "Modular restrictions on Mersenne divisors". Primes.utm.edu. http://primes.utm.edu/notes/proofs/MerDiv.html. Retrieved 2011-05-21.
- ^ http://www.jstor.org/stable/2972574 The American Mathematical Monthly, Vol. 18, No. 11 (Nov., 1911), pp. 195-197. The article is signed "DENVER, COLORADO, June, 1911". Retrieved 2011-10-02.
- ^ http://plms.oxfordjournals.org/content/s2-13/1/1.1.full.pdf Proceedings / London Mathematical Society (1914) s2-13 (1): 1. Result presented at a meeting with London Mathematical Society on June 11, 1914. Retrieved 2011-10-02.
- ^ The Prime Pages, M107: Fauquembergue or Powers?.
- ^ http://visualiseur.bnf.fr/CadresFenetre?O=NUMM-3039&I=166&M=chemindefer Presented at a meeting with Académie des sciences (France) on January 10, 1876. Retrieved 2011-10-02.
- ^ "Mersenne Prime Numbers". Omes.uni-bielefeld.de. 2011-01-05. http://wwwhomes.uni-bielefeld.de/achim/mersenne.html. Retrieved 2011-05-21.
- ^ The Prime Pages, The finding of the 32nd Mersenne.
- ^ Chris Caldwell, The Largest Known Primes.
- ^ The Prime Pages, A Prime of Record Size! 21257787-1.
- ^ GIMPS Discovers 35th Mersenne Prime.
- ^ GIMPS Discovers 36th Known Mersenne Prime.
- ^ GIMPS Discovers 37th Known Mersenne Prime.
- ^ GIMPS Finds First Million-Digit Prime, Stakes Claim to $50,000 EFF Award.
- ^ GIMPS, Researchers Discover Largest Multi-Million-Digit Prime Using Entropia Distributed Computing Grid.
- ^ GIMPS, Mersenne Project Discovers Largest Known Prime Number on World-Wide Volunteer Computer Grid.
- ^ GIMPS, Mersenne.org Project Discovers New Largest Known Prime Number, 224,036,583-1.
- ^ GIMPS, Mersenne.org Project Discovers New Largest Known Prime Number, 225,964,951-1.
- ^ GIMPS, Mersenne.org Project Discovers New Largest Known Prime Number, 230,402,457-1.
- ^ GIMPS, Mersenne.org Project Discovers Largest Known Prime Number, 232,582,657-1.
- ^ a b Titanic Primes Raced to Win $100,000 Research Award. Retrieved on 2008-09-16.
- ^ The largest known prime has been a Mersenne prime since 1952, except between 1989 and 1992; see Caldwell, "The Largest Known Prime by Year: A Brief History" from the Prime Pages website, University of Tennessee at Martin.
- ^ Paul Zimmermann, "Integer Factoring Records".
- ^ Chris Caldwell, The Top Twenty: Mersenne cofactor at The Prime Pages. Retrieved 2011-12-21.
- ^ Henri Lifchitz and Renaud Lifchitz. "PRP Top Records". http://www.primenumbers.net/prptop/searchform.php?form=(2^p-1)/%3F&action=Search. Retrieved 2011-12-21.
- ^ Alan Chamberlin. "JPL Small-Body Database Browser". Ssd.jpl.nasa.gov. http://ssd.jpl.nasa.gov/sbdb.cgi?sstr=8191+Mersenne. Retrieved 2011-05-21.
External links
- GIMPS home page
- Mersenne Primes: History, Theorems and Lists — explanation
- GIMPS status — status page gives various statistics on search progress, typically updated every week, including progress towards proving the ordering of primes 40–47
- Mq = (8x)2 − (3qy)2 Mersenne proof (pdf)
- Mq = x2 + d·y2 math thesis (ps)
- Mersenne prime bibliography with hyperlinks to original publications
- (German) report about Mersenne primes — detection in detail
- GIMPS wiki
- Will Edgington's Mersenne Page — contains factors for small Mersenne numbers
- a file containing the smallest known factors of all tested Mersenne numbers (requires program to open)
- Decimal digits and English names of Mersenne primes
- Prime curios: 2305843009213693951
MathWorld links
- Weisstein, Eric W., "Mersenne number" from MathWorld.
- Weisstein, Eric W., "Mersenne prime" from MathWorld.
- 47th Mersenne Prime Found
|
|||||||||||||||||||||||||||||
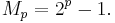
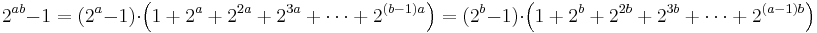
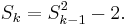
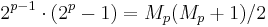
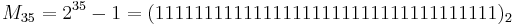
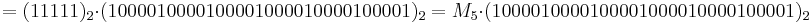
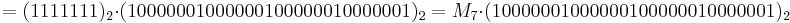
![=(11111)_2 \cdot (1111111)_2 \cdot [(1000010100101010010100001)_2 - (0100001010010100101000010)_2]\,](/2012-wikipedia_en_all_nopic_01_2012/I/ddbb735b6c62c771c31a4d69c17fb33a.png)